| Determina les mides d’una finestra d’arc de mig punt, sabent que el perímetre ha de ser de 10 m si es vol obtenir la superfície màxima. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 460 › ›
| En quin punt de la paràbola y = 4 – x2 la tangent forma amb els eixos de coordenades un triangle d’area mínima? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 441 › ›
| [IBO] Troba l’equació de la recta tangent a la corba y = x² que és paral·lela a la recta y = x |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 321 › ›
| Troba l’equació de la recta tangent a la corba y = x² que és paral·lela a l’eix horitzontal, troba també l’equació de la recta perpendicular a l’anterior i que passa per x = 1 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 317 › ›
| [IBO] Troba l’equació de la recta normal a la corba y = 1 – 2x², per x = -1 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 316 › ›
[IBO] Considera la recta tangent a la corba y = x³ + 4x² + x – 6
a) Troba l’equació d’aquesta recta al punt on x = -1
b) Troba les coordenades del punt on aquesta recta talla de nou la corba donada |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 315 › ›
La recta y = 16x – 9 és tangent a la corba y = x³ + ax² + bx – 9 al punt (1,7).
Troba els valors de a i b
› › Clica per a veure el vídeo d’ACTIVITAT 314 › ›
[IBO] La tangent a la corba y² – x³ = 0 al punt P(1,1), talla l’eix X a l’abcissa Q i l’eix Y a l’ordenada R.
Troba la ratio PQ/QR |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 313 › ›
| [IBO] Per a quins valors de m la recta y = mx + 5, és tangent a la paràbola y = 4 – x² ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 312 › ›
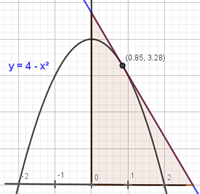
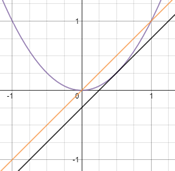
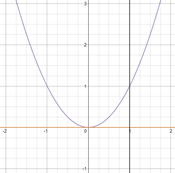
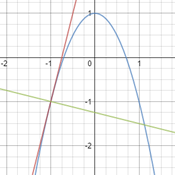
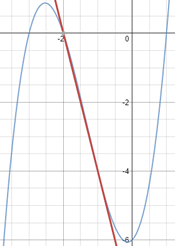
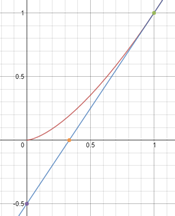
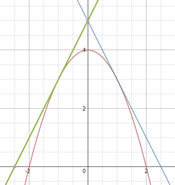
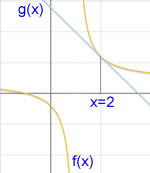
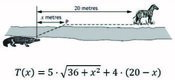
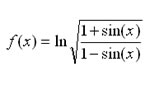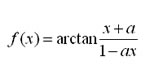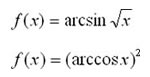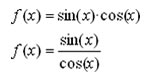Un cocodril vol capturar una zebra que està 20m més endavant però a l’altra banda del riu. El cocodril viatja a diferent velocitat a l’aigua i a terra. El temps que triga el cocodril en atrapar la zebra ve donat per la fórmula de la dreta.
Estudia 3 situacions:
1 – El cocodril no viatja per terra i segueix una línia recta a través del riu fins a atrapar-la
2 – El cocodril viatja, per l’aigua, la distància més curta possible
3 – Entre els temps que s’han obtingut en els casos anteriors hi ha un valor de x que minimitza el temps que triga el cocodril en atrapar la presa. Troba’l i digues quin és aquest temps. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 310 › ›
| Calculeu l’equació de la recta tangent a la corba f(x)=(x+1)/(x-1) en el punt d’abcissa x=2 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 305 › ›
| Calculeu l’equació de la recta tangent a la corba f(x)=3x² – 2x + 3 en el punt d’abcissa x=0 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 304 › ›
| Calculeu el valor de x que anul·la la segona derivada de la funció f(x)=e-x² |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 303 › ›
| Calculeu el valor de m perquè la derivada de f(x)=(mx+1)/(2x+m) per x=1 valgui -1 |
|
› › Clica per a veure el vídeo d’ACTIVITAT 302 › ›
|
|
