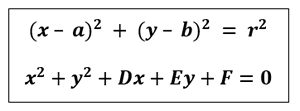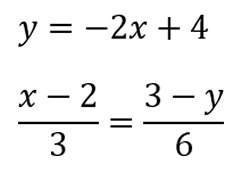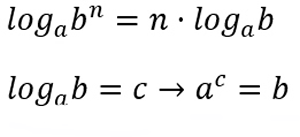Busca l’equació de la circumferència en els casos següents:
a) Té el centre a (1,4) i passa per A(-6,-1)
b) Té per diàmetre els punts A(2,3) i B(-5,2)
c) Passa pels punts A(1,0),B(3,-2)C(1,-4) |
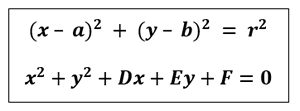 |
› › Clica per a veure el vídeo d’ACTIVITAT 609 › ›
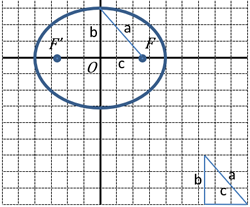
| Busca els eixos, distancia focal i excentricitat de l’el·lipse que té com a equació 9×2 + 16y2 = 144. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 608 › ›
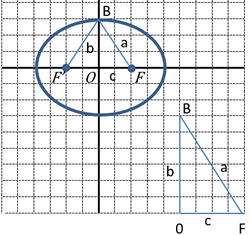
| Busca l’equació de l’el·lipse que té els focus F’(-2,0) i F(2,0) i que la suma de les distàncies a qualsevol n punt és 7. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 607 › ›
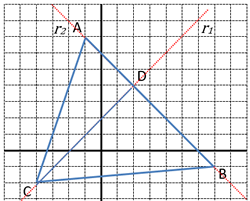
| Els punts A(-1,7), B(7,-1) i C(-4,-2), formen un triangle, troba la seva àrea |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 606 › ›
| Troba la recta mediatriu del segment d’extrems A(2,5) i B(4,-7) |
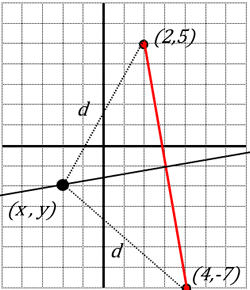 |
› › Clica per a veure el vídeo d’ACTIVITAT 605 › ›
Aquil·les persegueix una tortuga que li porta 990 m d’avantatge. Aquil·les corre a una velocitat de 10 m/s i la tortuga avança 1 m cada 10 s.
Quan de temps trigarà Aquil·les a atrapar la tortuga? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 603 › ›
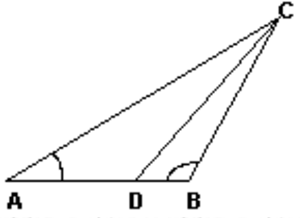
| La figura inferior mostra un triangle ABC en què l’angle A = 30º, l’angle B = 120º i la recta CD és la bisectriu de l’angle ACB.
Quin és el valor de la raó BC/CD ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 602 › ›
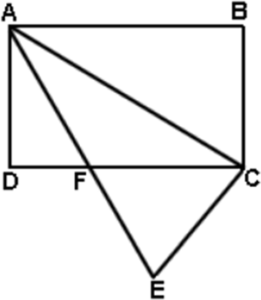
En la figura, ABCD és un rectangle amb AB = 16 cm i BC = 12 cm. ACE és un triangle rectangle amb AC ⊥ CE i CE = 15 cm.
Si F és el punt d’intersecció dels segments AE i CD, llavors quant val l’àrea de AFC? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 601 › ›
| [PERMUTACIONS AMB REPETICIO]
Dos coloms blancs i vuit coloms grisos que volen junts en bandada, es posen a descansar tots alhora en un fil elèctric, alineats un al costat de l’altre.
Suposant que s’han posat a l’atzar, quina és la probabilitat que els dos coloms blancs quedin un al costat de l’altre? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 600 › ›
| En uns grans magatzems han de determinar el preu de venda d’un jersei. Un estudi de mercat indica que si el preu és de 75 € es vendran 100 jerseis. També es pot pensar que per cada 5 € d’augment en el preu es vendran 20 jerseis menys, i que, en canvi, per cada 5 € que s’abaixi el preu es vendran 20 jerseis més.Suposant que es fabriquen tants jerseis com se’n venen i que el preu de cost de cadascun és de 30 €, quin serà el preu de venda que donarà uns beneficis màxims? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 599 › ›
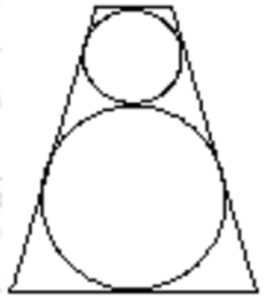
A l’interior d’un trapezi isòsceles de bases 9 cm i 1 cm, s’han inscrit dos cercles tangents, de manera que el radi del gros és el triple del radi del petit.
Quina mesura, expressada en centímetres, tenen els costats iguals del trapezi? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 598 › ›
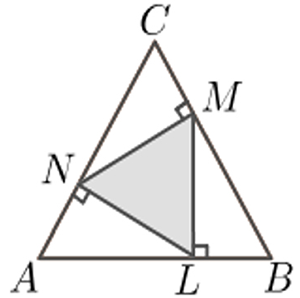
En els costats d’un triangle equilàter ABC, que té l’àrea igual a 36 cm2, hi ha tres punts N, M i L, amb la propietat que LM és perpendicular a AB, MN és perpendicular a BC i NL és perpendicular a CA.
Quina és l’àrea del triangle LMN? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 597 › ›
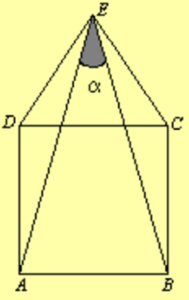
| A la figura, ABCD és un quadrat i CED és un triangle equilàter.
L’angle α és igual a… |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 596 › ›
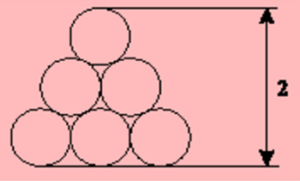
| El «triangle» de la figura està format per cercles tots ells del mateix radi r.
L’altura del «triangle» és 2.
Quina és la mesura del radi r? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 595 › ›
Quants nombres enters n són solució de la inequació
90n ≥ n2 + 2000 ? |
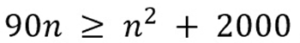 |
› › Clica per a veure el vídeo d’ACTIVITAT 594 › ›
[COMBINACIONS SENSE REPETICIÓ]
En un bloc de deu pisos, hem de pintar cada planta en blau o en groc, però dues plantes consecutives no es poden pintar de blau.
De quantes maneres diferents podríem pintar el bloc de pisos? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 593 › ›
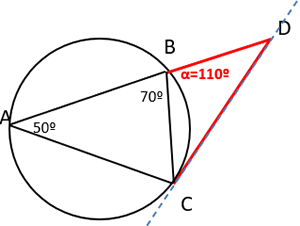
| Un triangle ABC amb A = 50º , B = 70º , està inscrit en un cercle.
La tangent a aquest cercle en el punt C talla la prolongació del costat AB al punt D.
Quant mesuren els angles del triangle BCD? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 592 › ›
Si log p19 = 20, troba log p2 191/2
Si log p a = 5 i log q a2 =12, troba log pq a3
Si log 2 10 = a, troba log10 2
Si log b a = c i log x b=c, troba log a x |
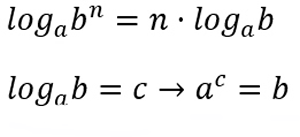 |
› › Clica per a veure el vídeo d’ACTIVITAT 591 › ›
Amb les 3/4 parts de líquid que cap en una ampolla és pot omplir un got i mig.
Quants gots omplirem si tenim l’ampolla plena? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 590 › ›
|
|