| La suma de n nombres naturals consecutius, presos a partir del 11 és 1715.
Troba el valor de n |
|
› › Clica per a veure el vídeo d’ACTIVITAT 47 › ›
| Les edats de quatre germans formen una progressió aritmètica, i la seva suma és 32 anys.
El més gran té 6 anys més que el més petit. Troba les edats dels quatre germans. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 46 › ›
| Dóna la solució en forma de desigualtat, interval i representació gràfica de la inequació de la imatge |
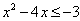 |
› › Clica per a veure el vídeo d’ACTIVITAT 45 › ›
| Trobeu les solucions de l’equació de 2n grau de la imatge |
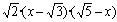 |
› › Clica per a veure el vídeo d’ACTIVITAT 44 › ›
| Una partícula que parteix del repòs descriu un moviment circular uniformement accelerat. Calculeu l’angle que ha girat en el moment en que els mòduls de l’acceleració tangencial és el doble que el mòdul de l’acceleració normal |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 42 › ›
Un automòbil circula a 80 Km/h, frena i s’atura en 10 s. Calculeu
a) Les voltes que faran les rodes si tenen un radi de 50 cm.
b) L’acceleració angular de les rodes |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 41 › ›
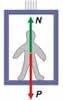
Una persona és a dins d’un ascensor al damunt d’una bàscula calibrada en Newtons.
a) Si l’ascensor puja amb una acceleració de 3,1 m/s² i la bàscula assenyala 744 N, quina és la massa de la persona?
b) En quina situació la bàscula indica 522 N?
c) En quina situació la bàscula indica exactament el pes de la persona?
d) En quina situació indica 0? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 40 › ›
| Quina velocitat angular s’ha de donar a una estació espacial de forma anular de 60 m de diàmetre per tal de crear una gravetat artificial igual a la terrestre? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 39 › ›
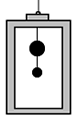
A l’interior d’un ascensor hi pengen dos objectes esfèrics de masses 2,3 Kg i 1,6 Kg el primer està unit al sostre mitjançant una corda, i el segon està unit al primer també amb una corda. Determineu la tensió de les cordes en les situacions següents:
a) L’ascensor arrenca pujant amb una acceleració constant de 1,1 m/s²
b) L’ascensor puja a una velocitat constant de 3 m/s
c) L’ascensor, que estava pujant, frena amb una acceleració de 1,2 m/s² |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 38 › ›
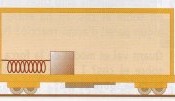
En un vagó de tren hi ha una massa de 250 g unida mitjançant una molla a l’extrem esquerre d’aquest. Si la molla té una constant elàstica de 15 N/m, i no hi ha fregament entre el cos i la superfície del vagó, determineu l’allargament que experiment la molla en les situacions següents:
a) El vagó es mou cap a l’esquerra amb acceleració constant de 1,6 m/s²
b) El vagó es mou cap a la dreta amb acceleració constant de 2,8 m/s²
c) El vagó està en repòs |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 37 › ›
Dues masses pengen unides per una corda en un pla inclinat, una per la rampa i l’altra penja per l’extrem del pla. Es considera que no hi ha fregament i que la massa de la corda es negligible.
a) Quin ha de ser l’angle d’inclinació del pla, si m1= 29 Kb (la de la rampa) i m2= 17 Kg (la que penja de l’extrem) i el conjunt es mou amb una velocitat constant
b) Si l’angle del pla inclinat és de 30º, quina ha de ser la relació entre unes altres masses perquè el conjunt es mogui amb una velocitat constant? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 36 › ›
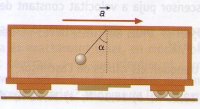
Un pèndol es construeix amb una corda de massa negligible i amb una bola de massa 525 g. El pèndol penja dels sostre d’un vagó de tren, que porta una moviment rectilini uniformement accelerat. El pèndol està inclinat un angle α respecte la vertical.
a) Per què esta el pèndol inclinat respecte a la vertical?
b) Suposem que l’acceleració del vagó és constant i val 3,2 m/s². Calculeu l’angle que forma la corda amb la vertical.
c) Calculeu la tensió de la corda. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 35 › ›
[PAAU 1999] Tenim dues masses iguals de M= 5Kg penjades pels extrems d’una corda que passa per una politja (màquina d’Atwood). Les masses de la corda i la politja es poden considerar negligibles. Inicialment les masses estan en repòs.
a) Considereu una de les masses M. Feu un esquema de les forces que hi actuen i indiqueu sobre quin cos estarien aplicades les forces de reacció corresponents
b) Sobre la massa penjada de la dreta hi cau un tros de plastilina de massa m= 500 g que s’hi queda enganxada. Quina serà l’acceleració de les masses en el moviment posterior al xoc?
c) Quins són els valors de la tensió de la corda abans i després del xoc? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 34 › ›
Una caixa de 15 Kg de massa descansa sobre una superfície horitzontal que presenta un coeficient de fregament estàtic de valor 0,45, i un coeficient de fregament dinàmic de 0,42. Per moure la caixa, l’estirem amb una corda que forma un angle de 20º amb l’horitzontal.
a) Quina força mínima hem de fer perquè la caixa es comenci a moure?
b) Quina força hem de fer per moure la caixa amb velocitat constant?
c) Si la força amb que estirem la corda val 65 N, amb quina acceleració es mou la caixa? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 33 › ›
| Resol el sistema d’equacions de 1r grau amb dues incògnites, per reducció i també gràficament que veus a la imatge |
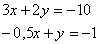 |
› › Clica per a veure el vídeo d’ACTIVITAT 32 › ›
Un número està format per dues xifres consecutives, on la 1a és la més gran, de tal manera que si escrivim el número a l’inrevés, resulta que el quadrat del número obtingut és 209 unitats mes gran que 10 vegades el número inicial
a) Quin número és? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 31 › ›
En Joan li diu al Pere, si em dones una moneda tindrem les mateixes. I en Pere respon si me la donessis tu a mi aleshores jo en tindria el doble que tu.
Quantes monedes tenen cadascun? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 30 › ›
Converteix a fracció de números enters :
a) 12,75
b) 12,757575…
c) 12,3757575… |
|
› › Clica per a veure el vídeo d’ACTIVITAT 29 › ›
| Calcula 8:(-4) + 3·[(-2)·[-1) + 3·((-1) + 2·6:3)] |
|
› › Clica per a veure el vídeo d’ACTIVITAT 28 › ›
|
|